This is Naked Capitalism fundraising week. 1528 donors have already invested in our efforts to combat corruption and predatory conduct, particularly in the financial realm. Please join us and participate via our donation page, which shows how to give via check, credit card, debit card, or PayPal. Read about why we’re doing this fundraiser and what we’ve accomplished in the last year, and our current goal, more original reporting..
Yves here. I know I’m showing my age in recoiling at the remarks in this post that show how much educators see the purpose of college being to land a particular type of job, as opposed to create well informed citizens who also have skills that employers can put to use. As for the value of computer science degrees in particular, it’s been true for a long time, and it may still be true, that entry level jobs are scarce because employers send what used to be yeoman’s tasks overseas or use workers on H1-B visas. So one has to wonder why tech squillionaires are teaming up to have US schools create even more coders.
But the main point of the article is important too: individuals need a certain level of math skills to perform at a competent level in many jobs. Giving math credits for computer science may enable too many to skip foundational training.
By Chris Orban, Assistant Professor of Physics, The Ohio State University. Originally published at The Conversation
In 2013, a who’s who of the tech world came together to launch a new nonprofit called Code.org. The purpose of the organization was to get more computer science into schools.
Billionaires like Mark Zuckerberg and Bill Gates donated millions of dollars to the group. According to the organization’s last annual report, Code.org spent more than US$91 million between 2013 and 2018. Of that amount, $6.9 million went to advocate for state legislation across the country.
As part of the organization’s mission to “make computer science count” in K-12 education, code.org takes credit for having influenced graduation policies in 42 states. Today, 47 states and the District of Columbia allow computer science classes to count in place of math classes like Algebra 2. Prior to the organization’s work, only a few states allowed computer science to count for math credit.
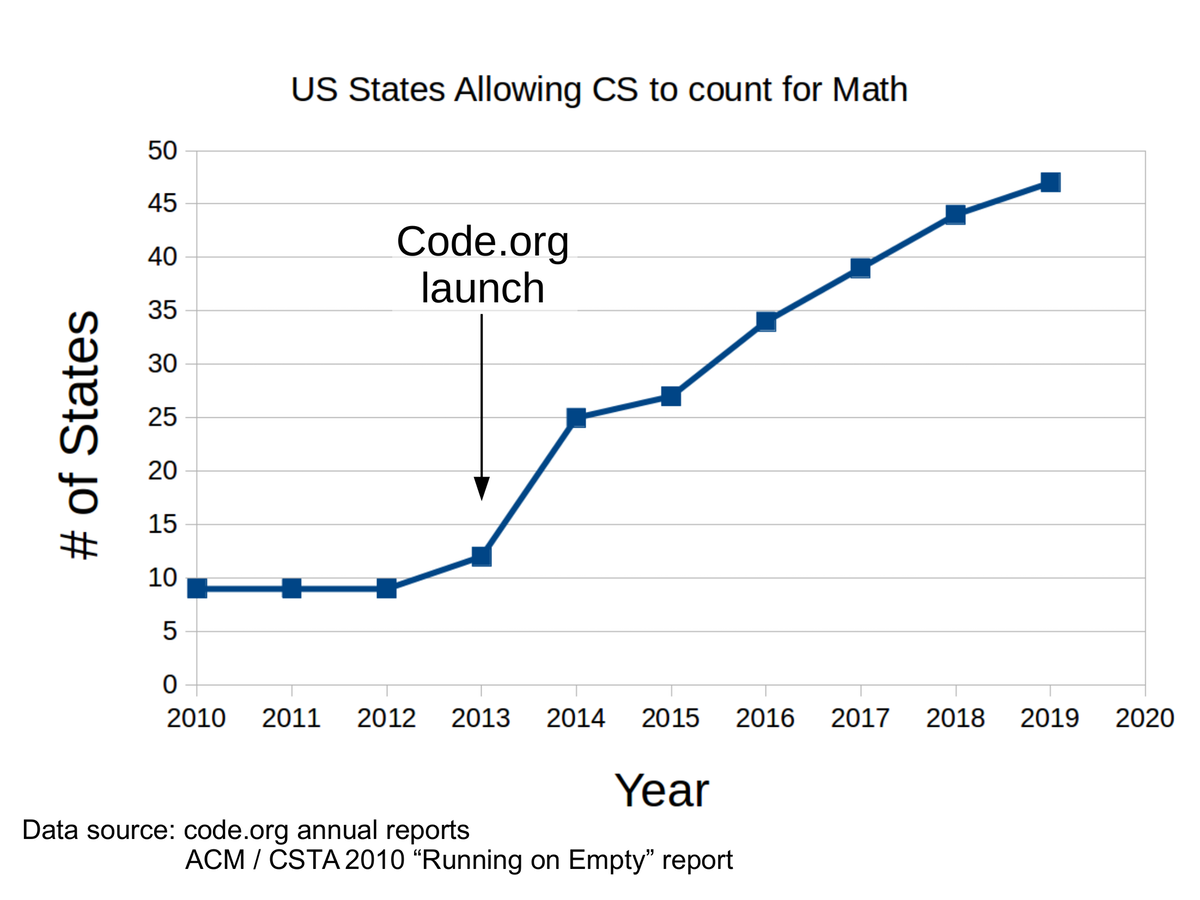
In addition, 29 states passed legislation allowing computer science to count in place of a science course. When computer science begins to count as math or science, it makes sense to ask if these changes are helping America’s students or hurting them.
Is This a Good Idea?
As a computational physicist and education researcher who teaches college freshman introductory physics, I worry that allowing computer science to count as a required math or science course could make students substantially less prepared for college. I searched around for research on this topic and asked several colleagues but came up empty-handed. I also worry that a lack of math and science preparation in high school could artificially narrow the range of options for students who might otherwise have promising STEM careers.
Certainly, computer science is important to teach in high school. I lead an effort called the STEMcoding Project where I have trained a few dozen high school math and science teachers to integrate coding into math and science, and I have worked with a few high school computer science teachers to integrate more science and math into their curriculum.
I began working on the STEMcoding Project in 2016 after getting frustrated by how many undergrads and even graduate students came to my office wanting to be mentored on a computational physics research projects despite having no prior experience with programming.
When I consider computer science in schools, I want to know: What kind of computer science, how rigorous is the content, and what ends up being removed to make room for it? Although there are exceptions, most high school computer science curricula that I have seen have been light on math and science.
I worry that students may take computer science just to avoid the more difficult math and science courses they need for college. Computer science could be a way for students to circumvent graduation requirements while adults look the other way.
Others are concerned, too. In response to these trends, the National Council of Teachers of Mathematics called in 2016 and as recently as 2018 for math classes to count as math only when they are “designed explicitly to teach mathematics.”
Career Preparation
Computer science can be a practical class that helps prepare students for real middle-class jobs. Florida Governor Ron DeSantis expressed similar ideas when he signed a workforce education bill into law earlier this year that allows computer science to count as math or science.
 Florida Governor Ron DeSantis signs a workforce education bill that allows computer science to count as required math course. Florida Governor’s Press Office
Florida Governor Ron DeSantis signs a workforce education bill that allows computer science to count as required math course. Florida Governor’s Press Office
“Other than trying to keep my kids from falling down the stairs in the Governor’s mansion I don’t know how much I deal with physics daily,” the governor said. But he said it’s different when it comes to computer science. “You cannot live in our modern society without dealing with technology or computers in your daily life,” he added.
There are some solid numbers behind this sentiment. Despite a surge in the number of students taking computer science in college, there is still far more demand for computer science and software engineering workers than there is supply.
Perhaps because of this demand the salaries for computer science jobs are estimated to be as much as 40% more than jobs in other fields.
Are Important Math Skills Lost?
Despite these arguments there are still good reasons to question computer science substitution policies like the one deSantis signed. Being a modern electrician, for example, requires some understanding of algebra and trigonometry.
Even for those who plan to study computer science, taking Algebra 2 and above is highly recommended. Algebra 2 and other advanced math courses are also important for engineering.
Some studies estimate that a remarkable 40% of college freshmen in the U.S. require remedial math courses. That portion could go up if fewer students are taking a traditional math sequence in high school.
Taking remedial math courses like Algebra 2 in college requires students to spend more time and money than they would if they just took and passed four years of math in high school. According to one study, only about half of all students who take remedial math ever complete it. So skipping Algebra 2 in high school could end up stopping many students from graduating from college at all.
A Matter of Choice
Perhaps in weighing these concerns, of the 47 states that do allow computer science to count in place of math, 13 leave it to individual districts to decide whether to let students exercise that option. The list of 13 includes tech savvy states like New York and California.
In a majority of U.S. states, students and families now have a serious choice to make. Students can take a nontraditional route and replace courses like Algebra 2 and physics with computer science, taking their chances that this won’t come back to bite them later. Or they can stick with a more traditional curriculum, with its traditional advantages and disadvantages.
As computer science substitution policies become more widely utilized, I plan to research whether or not these CS substitution policies help more than they hurt.
We especially need to understand how this flexibility affects women and students from underrepresented groups. Computer science advocates have created a kind of national experiment. The next few years will show if this was a good idea, but only if we’re looking at more than just the numbers of students taking computer science.


Real computer science (which is NOT coding) is a collection of a few math branches. But a very specific ones.
Giving math credits for CS is like giving general math credits for descriptive geometry – useful, but specialised.
What I see around myself if way too much of “maths is hard, let’s figure out how to drop it”. That then leads to the more obvious “what do you mean you have no idea what a percent is?”, but also to the general inability to deploy logic. And no, logic by itself is not good. But logic is what you need to build critical thinking, and properly taught maths is, first and foremost, about critical thinking – because unlike most of the other sciences, all the experiments can be done with a bit of paper and your head. And it is strong enough to be able to show its own weaknesses (Goedel) and grow with it.
I think it applies to almost any subject that when you try to teach the ‘practical’ applications without the theoretical underpinnings you are creating the potential for entire bodies of knowledge to go astray.
The biologist EO Wilson made this point some years ago when he criticized the insistence on all post-graduate scientists having to use statistics. He argued that too many bad papers were passing peer review because the authors and reviewers ‘knew’ statistics in a superficial practical manner which can lead to undue confidence in the results – ones which specialist statisticians would not accept. Subsequent replication crises in a number of sciences would seem to confirm he had a point. Lars Styl makes similar arguments in his blog, specifically about economics.
Don’t get me started on statistics.. I won’t. I won’t. I WONT!
OK, I will. A lot of what passes for science now is not science, it’s crap based on misunderstanding on tools. Someone, somewhere, had the bright idea of telling ‘scientists’ about linear regression and hypothesis testing.
It’s like giving kids keys to the car without teaching them how to drive. It can work, but it can kill people too.
83.2% of the people I asked said statistics is a science so there.
Umm, very good example
What was the standard deviation?
What were the ages, sex, and educational achievements of the people sampled?
etc, etc
And the list of criteria which defined the answer goes on and on.
Should I feel bad that it took me a moment to get the joke?
+1
My wife and I both work in Institutional Research–she is the head of the department for a college, and has to hire often. The job requires knowledge of statistics (clear in the job description).
More than half of her applicants have no knowledge of statistics, but think they do because they know how to do a regression in R.
Computer Science :: Math as Cook::Chef?
Pretend that they are equivalent, but no new recipes or theories get produced. Someone has to do the heavy lifting and stirring and thinking beyond picking up a handheld device and searching for an answer that might appear correct.
Bring back long division.
…fractions, too!
So what’s a common denominator for folks wanting to skip Math? A less than fluent instructor in high school. Math has a hierarchy, miss one of the stones in the pyramid and you’ll struggle.
‘More than half of her applicants have no knowledge of statistics’
Maybe they can ask Siri-
https://www.youtube.com/watch?v=Uo0KjdDJr1c
I think EO Wilson falls into a semantic trap and confuses a “practice” of generating statistical models with the effective (“practical”) value of the models. His point is important, his conclusion that the practice is bad because of misunderstanding theory is arguable, especially since some of the problems were discovered in practice, not in analysis of the application of theory.
That theory must be understood first and that understanding theory insures effective practice is not demonstrated, and is easily challenged: most people don’t comprehend walking/running as applications of theory but they can perform them quite well. It could be said that Wilson makes a similar categoric error to the one he is critical of. It’s unfortunate because his original complaint is important and shouldn’t be discarded.
+1. I was going to write something similar but not as clear.
But, if say, Knuth’s The Art of Computer Programming is the text, I’m probably fine with it.
I agree that you can use CS to teach thinking, but I’d say that it’s more restricted than maths. The problem with code (and with some IT/CS people in general) is that the code is precise, but restricted. Code is law is better “in CPU, code is the law of nature”.
Maths on the other side is precise, but way less restricted (starting with irrational numbers etc…).
David Hilbert is said to say of one of his students who left to become a poet: “I can’t say I am surprised. I never thought he had enough imagination to be a mathematician.”
I could not do ‘math’ in school, neither arithmetic nor algebra, except for geometry, which had proofs. Proofs — at least ‘originals’ — were like composing Latin prose, which I enjoyed and was good at. However, the first time I saw a computer, then a room-filling object, with parts that did things with no one around, I knew what it was. Utterly uncredentialled, I contrived access to one as an operator and was writing working code in a few days. I immediately turned this opening into the beginning of a lucrative and comparatively enjoyable career. In those days one had to program everything, because there was not much logical or physical infrastructure, so it was quite an exercise of one’s mental capacities. I don’t recall anything I had learned in school as being of the slightest use, except the same common arithmetic we have to learn to do carpentry and cooking. However, I did later use the skills I had acquired from programming to enter upon certain kinds of math as entertainment. In spite of the grinding awfulness of arithmetic and algebra, I had learned through ‘coding’ that I could conquer and exploit them, and even make the machines do a lot of the dirty work..
Later, one of my relatives went through a ‘computer science’ major. She was forced to learn circuit design and calculus. In a 50-year career, I never had to use either of these, although I once used a bit of thumbnail calculus to show a colleague that his guess about a particular channel capacity problem was too low. I don’t what is taught in school now, so things may have improved. Or deteriorated, I suppose.
Yves says: ‘I know I’m showing my age in recoiling at the remarks in this post that show how much educators see the purpose of college being to land a particular type of job, as opposed to create well informed citizens who also have skills that employers can put to use.’ — I went to a prestigious Eastern university for a while in the late 1950s, and that’s all that most of the students were doing there. I suppose they sometimes learned things by accident. No one wanted you or anyone to be a well-informed citizen, quite the other way around. I don’t know if things have changed that much. It doesn’t seem so.
Geometry was the only one I really liked either, but code is an entirely different skillset than math, but it requires critical thinking and is helped greatly by it. It’s not the shiny you put on your resume to attract attention in a world obsessed by such, it’s the real workhorse though.
Anyway if someone is just really bad at math and just wants to get out of it, I might just suggest a small liberal arts college that doesn’t require it. I know people who never graduated college solely because of the math requirement but had a lot of other areas they were good at. If they had thought more broadly about their possibilities (ie maybe big state school with boatloads of math requirements really isn’t the only path, though it’s often the most affordable path) this may not have been the case. It’s kind of a waste really.
I think coding is a good way to teach logic and checking work. Nothing is more immediate feedback on faulty logic or attention to detail than a program that spins in circles or crashes. It is not a substitute for math, but another branch of it, similar to Euclidean geometry as somebody mentioned above. So allowing coding as a quarter of somebody’s math curriculum is fine with me (I am an engineer), but it is like any math subject – if you only do one type of math, you are missing much of the overall world view.
yes it’s fine for teaching logic and checking work, and testing out hypothesis (in a limited sense), and logically getting to the bottom of problems etc.. I suspect anyone who thinks otherwise has never seriously done coding period and has a very superficial understanding of it.
It doesn’t mean you are an expert on any other math subject of course, you actually need to study them to be. I mean duh. It’s about like saying studying art history doesn’t make you an expert in psychology …
And yet people continue to diss philosophy and formal logic.
Roger Penrose said an interesting thing in The Emperor’s New Mind. He said that he loved math and he was a natural at it and because it was so precise he assumed that all the other math students would think more or less the same way about the same problems. But he found just the opposite – that there is more diversity among math thinkers that any other branch of study. That hardly any two people could agree exactly on what their computations were doing. Most interesting.
Instead of TAOCP, I’d suggest Concrete Mathematics by Graham, Knuth and Patashnik. It’s a lot more suited to teaching and studying whereas TAOCP is more reference if you understand the wooly distinction I’m trying to make.
I think a big pain point for many kids is how math is taught. I always did well in math because I got it at a level most don’t appreciate (or at least eventually I did). The world became a set of curves when I learned calculus; and then everything became a set of lines when I learned linear algebra. But most people don’t leave math class and then see everything around them as foundationally mathematical. With that said, there’s a push here in the US to bring back shop class requirements. Personally I think it needs to come back and be integrated into math and science classes. Shop is nothing more than applied math and science. This is how you’ll get people who are not like me to really get a better grasp of math. How many construction framers realize they’re using trigonometry to cut crazy angles to frame a roof? I can remember once in high school, before the light bulb went off, asking a math teacher why I needed to know this crap? I now pay my bills because I have a huge mathematical background and I couldn’t do my job without that foundation. Getting kids to make some applicable connection would go a long way to keeping kids in math classes.
On a related point, I now have kids of my own and I cringe when I hear them say they can’t do it and they can’t count on their fingers – the teacher told them they aren’t allowed. I’m almost 50 and probably have taken a minors worth of college level math and statistics classes and I still use my fingers. For me it’s the visual thing. Sometimes I need that visual reference point. If I don’t have paper near by I’ll write equations in the air, just so I can visualize what I need to do. Telling kids they can’t count on their fingers is the first step in preventing them, or at least some of them, from being able to connect with math. And it’s taught that way not for the students benefit but likely because the teacher doesn’t see math the way that kid might.
Light bulbs go “on” to illuminate. Pet peeve.
You are right about counting on one’s fingers. I’ve taught octal and binary by starting with decimal (“How does an octopus count? Spread your fingers on your desk. How many fingers do you count? Now, hide your thumbs. How many fingers do you see now? That is how!”)
Can you encourage them to hold out for two pieces of calamari later instead of one now?
I remember reading somewhere recently that counting on fingers is a highly essential part of learning the mathematical process and kids who are dissuaded from doing so end up performing worse on math latter in life.
Teaching some physical disciplines (martial arts), I’ve found that people who have never climbed a tree lack certain abilities of coordinated movement that create a ceiling to the skill levels they can achieve. We actually coached several such students to climb a tree; some refused or gave up, those who did it just a couple of times were able to progress further.
Also, sadly, those who suffered profound neglect in childhood often exhibit poor hand skills, for lack of good example modeled by adults. Such training requires only minimal engagement by adults, children are eager to mimic and acquire practical examples of manual (and general physical) skill. Of course, some variation is normal.
Kids who count on their fingers — fast!
https://en.wikipedia.org/wiki/Chisanbop
Have your kids read Isaac Asimov’s book, “On Numbers”. It’s stories about math, measurement, counting, and the calendar.They’ll probably learn more there than in school (K-12).
“But logic is what you need to build critical thinking…” YOU GOT IT!
And logic doesn’t necessarily come along with math. Try developing logic with, say, the study of Latin or Greek in high school. Or even the critical review of fiction. Math bored me to sleep in high school. Language did not. And I got on the coder train late in life at the age of 35.
Two of my own kids slept through Algebra 2. One becoming an engineer, the other a kick ass elementary school teacher for “troubled” inner city schools. Neither of them fell in love with a computer before getting out of high school. Somehow they were able to develop the critical thinking skills.
Logic is math. Technically, grammars are math too!
The problem often is not with the math, but with how people were introduced to math. But, TBH, this is not only a math’s problem, but a general. A teacher can make or a break one’s love for a subject.
Teaching math well is actually hard. The beauty of language, song or a picture is obvious to most, and can be made attractive/interesting easily enough in most cases. But to be able to show beauty in abstraction is way harder. So it’s being taught like a tool, like being able to put down letters and put them into words. But while a letter is a letter is a letter, maths is way more than being able to add up your bill.
I’m not saying that maths is necessary for critical thinking skills – that’s clearly wrong. But at the same thing, maths is the critical thinking in the purest form, so if taught well, it can be incredibly powerful.
Re CS – what is often being trained as CS now is not really science, but more 21st century craft.
Which is not to say it’s bad, but it’s not a science. A 17th century lens manufacturer was (usually, people like Hooke aside), an exceptional craftsman. But he wasn’t a scientist. So taking CS craft-courses and giving credits for them can be like giving physics credits for blacksmithing.
“A teacher can make or a break one’s love for a subject.”
This basically sums up what I came here to say. My father is a mathematician, & I come from a small college town, so I grew up with a healthy appreciation (not quite love, that came later) for the subject, especially algebra; but every teacher I had until middle school prefaced math lessons with something along the lines of, “I hate math and I’ve never been good at it, it’s an innate talent and not a learned skill, you’ll never use anything you learn past arithmetic unless you’re a scientist, anyway, here’s the lesson.”
In response to Vlade’s first post: I think this is a very fair observation. REAL CS is not coding. When I took an MS in Computer Science — at OSU, ironically enough — it was enough like math to be very challenging to someone like myself without a sufficiently rigorous background. (Liberal Arts major here.) It is a specialized subset of math-related subjects — which in computation theory verges on mathematical logic. The coding part, i.e., programming work done mainly in prerequisite courses, was the easy part. (The challenge there was largely in being required to shift rapidly between operating systems and languages.) When it came to pure class work — computation theory, algorithms and complexity, formal programming languages, computer architecture, and operating systems — this career-changer in his forties found it a pretty tough nut to crack. All the more frustrating then when the software world I wanted to enter seemed to consider the move from one language to another as something akin to a brain transplant.
Yes, it’s an excellent idea. Coding improves your math skills, especially in geometry and logic, VASTLY more than a teacher drawing Euclidean proofs on a blackboard. Doing other REAL LIFE activities that require math, from gardening to cooking to carpentry, also improves your math skills VASTLY more than memorizing formulas.
Theory is NOT the foundation of math. Theory is just a decorative flourish tacked on after real math has been developed by real experience.
“Theory is NOT the foundation of math” Huh? Your understanding of what’s math is pretty poor..
The parts of math where theory becomes important (i.e. you have to prove stuff rigorously because intuition and experiment are both too unreliable) are way beyond what most people see in HS or college, including science majors. Until the 20th century, mathematics itself didn’t include much of what we now call theory.
Proving theorems is good for training reasoning skills that were traditionally part of philosophy, which nobody studies any more, and in math they are an object of study in their own right. But if you go up to a working scientist who uses vector calculus and probability all day long, they probably won’t know how to rigourously prove the basic theorems of those subjects. They teach that stuff in physics (etc.) classes in mathematically non-rigorous ways and that is fine.
Is there even such a thing as a high school philosophy class? I went to a fairly good high school but I don’t think it had one. THAT is something that should possibly be fixed. It would also be worthwhile if more people studied formal logic in college, though it’s hard to see how to do that in high school.
I don’t disagree with that, but that’s not the same as “Theory is NOT the foundation of math”.
IF the author said “teach applied math”, I could go with that. I do think we should teach some abstraction and abstract thinking (both precise in the maths sense and more philosophical), but I could go with that.
But saying that theory is not important in math is just nonsense. And, as per my post above on statistics, if we ignore the theory (which helps us to understand what are the limitations and correct uses of a tool), we can do more bad than good.
Maybe it would be helpful to define ‘math’, ‘theory’, ‘computer scince’, ‘coding’, and so on. Historically, most theory of any kind seems to have emanated gradually from practical experience; that seems to be the way humans learn new things. In grade school I was taught that 2+3=5, but if I asked why 2+3 always = 5, I would have been told to shut up and memorize it, not to consult the works of Professor Peano, which historically speaking were only a very recent addition to the knowledge of 2+3=5.
I oversimplify, of couse.
can’t agree with that. don’t skip the hard math.
you can’t do CS without math anyway. CS is not programming, just like EE is not soldering circuits. Both ☆are☆ math, in what sets them apart from the associated tech work. Ditto mechanical and chemistry, in its more interesting parts.
how’re you gonna explain something like system stability, without a few years of trig and calc and linear algebra and complex numbers, just as the bedrock foundation before actually getting to the tools used to analyze the problems (which can then refuce a formerly impossible task to 30 minutes the first time, 30 seconds in a spreadsheet if done repeatedly with varying parameters).
Maxwell used Faraday’s elegant drawings of his electromagnetic experiments to develop his mathematical theory of electromagnetism. He likely wouldn’t have done it without Faraday’s extensive and brilliant experiments, but Faraday never learned much math (he was largely self-taught in everything) and he would have just had books filled with pretty pictures and some fundamental findings (like light could be impacted by magnets) but without the unifying theory.
So theory and practice have to go hand in hand at some point.
It all depends on the content of the course so it seems difficult to have an informed opinion. However, this quote is a cause of concern for me:
That quote might indicate what might be in the course, possibly the content might be similar to the ECDL: http://ecdl.org/
My opinion of the ECDL is that it provides jobs for the trainers of the courses for ECDL, it keeps unemployed and/or young people busy and for some then it might actually have some practical use as well.
The basic answer is “it depends”. The usual “nerd” HS math sequence like I took has 5 classes (Algebra 1 and 2, Geometry, Pre-calculus, and Calculus). You’d either skip Algebra 1 (because you had it in Junior HS) or you could take Algebra 2 and Geometry at the same time. Plus you’d get some additional math if you took chemistry or physics.
I think substituting CS for some of the math can work ok if the CS curriculum is designed to actually cover some of the math topics it replaces. Much stuff from Algebra 2 could be lost without being missed (who remembers what synthetic division is?). Trigonometry’s relevance nowadays is because of how trig functions show up in calculus, so if that is put off into the pre-calculus class that is fine. Pre-calculus as I took it was a weird and useless class that covered a bit of linear algebra, a bit of complex numbers (but uselessly since without calculus), and a little bit of abstract algebra. There was also geometry which was mostly about Euclidean-style proof writing, i.e. its purpose was to teach reasoning skills rather than the theorems themselves, which are useless. But programming also does a good job of some of that.
This could be re-arranged some so in a 2-part CS class you’d do some numerical linear algebra and calculus, geometry could be mostly ditched, pre-calculus could be partly merged into CS 2 and otherwise rearranged to ditch some algebra and cover some logic, and calculus could stay about like I remember it but with some programming built in (basic numerical methods).
One thing I’d like to know is where they are going to get the teachers for this, since anyone qualified can probably make a lot more money as a programmer, in addition to not being treated like sh*t.
Why do I only see dollar signs here?
Let’s see, math requires a textbook, pencil, erasure and the discipline to learn a formal language that has developed over many centuries. These mathematics classes are the necessary foundation for learning any computational theory. Efficient code requires a knowledge of algorithms which will be unpenetrable without a solid foundation of mathematics and statistics.
A high school computer science class is great for locking in students to proprietary software and hardware. Apple and Microsoft must be pushing this substitution idea furiously behind the curtain.
Learning math gives one a tool for life. Learning one particular programming language on one hardware platform does not without a solid math background.
There is something to be said for the idea that “CS” in this post’s context is a grift for getting more expensive corporate computer shit into classrooms instead of improving conditions and pay for teachers.
As someone who did computer programming in high school back in the mid-1970s, we were taught BASIC, COBOL and FORTRAN languages along with the usual Algebra I/II, Geometry, Pre-Calculus and Calculus. At the college level at that time, Computer Science was split between Arts, Sciences and Letters along with Engineering and Business.
At my current employer, we do our own entry-level programming training for legacy core systems as the platforms they live on (IBM mainframes) are no longer taught at colleges and universities. I also participate in semi-annual meetings with a statewide college system to go over their curriculum and what they are currently teaching and what should they be teaching.
The question always comes down to this: What is the best course to take – teaching coding to someone who knows the business or teaching the business to someone who knows how to code?
Computer science can be described as math in motion. The fundamental parts of computer science are based on many branches of mathematics. Boolean algebra, graphology, numerical bases, alternative numbering systems come together to form the ideological blocks of computer science. Which has led to advancement of many different fields of science at an incredible pace. Could you imagine a radio astronomer performing Fourier transformations with pencil and paper? The pace of discovery would slow to a crawl. Intermingling fundamentals of computer science with basic math at a young age would help young people to understand that math isn’t just numbers, but an incredible tool that can be used to improve the world and make sense of a confusing world.
In this sense, computer programming amounts to a far more powerful pencil. It is a tool for solving problems that invariably come from another domain. If that domain is accountancy, you need to have the basics of that, if that domain is time/distance/speed, then you need to know Newton and his math – or Einstein and his math, depending on how closely you approach cosmic speeds and distances.
When you learn to use a pencil, what are you learning? It goes along with language development, or artistic drawing, or arithmetic or other applications of that tool. When you learn computer programming you program an application, as above. Serious computer programming is also a discipline that confronts you with the benefits of proper planning and preparation, or bedevils you with their lack.
“Computer Science” is a grab bag of courses hung around computer programming, intended to provide some of the applications. Of course some people at college , woho find the mental organization required for proper computer programming ‘hard’, manage to get through the course and even graduate, without ever being fully able to conceive, write, debug, run and document a serious program. That is a whole phalanx of people for whom “CS” should NOT be a substitute for math or any science.
(I got my Computer Science degree in 1980, when we had to learn to program ‘on the bare metal’!)
I am in Yves’ camp: training and education are different, but today the terms are interchanged. I strongly believe schools should be a place for education. Okay, some students have low (math) aptitude as I know from tutoring and that should be acknowledged as courses available for them, but math should not be confused with CS. Appoligies to true computer scientists for the misuse of the term CS here and below, but CS as used in this discussion is equated with programming, and so I shall misuse this as well.
CS is meth, math is thinking. Programmers get a rush from seeing their programs compile and run. Little hard logic is required for this, only resolving compiler errors and code crashes. It is analogous to providing positive feedback, regardless of performance.
CS is LSD. I have witnessed over my 40 years of computer applications where more and more and more and more of code and upgrades are based on the GUI. Fancy screen displays using available primitives (like x-windows, openGL) dominate a coders time and the Gee-whiz is the display and not the underlying computation.
CS is lazy, math is rolling one’s sleeves up. I have seen innumerable times where ‘if statements’ are a lazy approach to code flow or calculations which could have been better handled by math, whether it is Boolean logic or algebra. The danger of if-statements is that it increases untested paths through the code and hence underlying errors remain.
More and more tools are off-the-shelf and available, reducing the demand for thoughtful understanding. Math related include computational algorithms that exist for most everything: linear algebra (i.e. matrix), differential equations, Fourietc etc transforms, statistics. Additionally, engineering and math packages such as Matlab are taught and encouraged to be used even in college engineering disciplines such that students can readily get ‘results’ without understanding anything about what’s happening.
Re. the reference to bringing back shop classes: I overly strongly support this. As our children went through school, shop changed from hands-on to using computer simulations of design and such. Our first had to put a lawnmower engine back together, and the last used a computer to see how launch angles changed distance. Shop should stay in the physical world. With the lawnmower it either works or it doesn’t. A computer program can give absolute rubbish – and that is considered ‘working’. NOT.
I shall stop, as my rant could continue forever. Viva la educacion.
“math is thinking”
Not in Seattle, there math is “power and oppression” and seemingly racist, at least according to the Seattle public school district’s K-12 “ethnic studies framework” for teaching mathematics:
https://www.k12.wa.us/sites/default/files/public/socialstudies/pubdocs/Math%20SDS%20ES%20Framework.pdf?fbclid=IwAR3z228kLBOJgz2NaBN3l5Dn0TjXbvjtXfH5WsyBMjr-_13rOLp_mZ1mXb0
Wow – that is some rather unintentionally hilarious bureaucracy right there.
Absolutely not, don’t skip the math. don’t skip the “CS” either, though what they mean by cs is usually not. you will eventually need both if you want to do the real thing in STEM.
Start young. They start way too late in the US educational system. you can (at the expense of social skills) learn all of elementary and high school math and science, and more, in 8 years rather than 12. doesn’t have to be that extreme, but most American kids learn jack sh#t in elementary school, wasting the best learning years in a human life cycle.
with “CS” too you can and should start young. that does NOT mean teaching an 8 or 10 year old to program Java or whatever, it means solving puzzles and free play. “Logo”, if anyone remembers that. Figure out the snowflake, the fern, etc. If you want to mess with them, ask how much one weighs. Let em make a little game, just play. When a bit older, Scheme. After that it will self teach til college, so go back to math.
K-12 is circling the drain. CS, done properly, could enhance mathematical understanding. However, given my experience in the K-12 system, it will be poorly implemented. The pressures will make it so. From the imposition of bizarre standards and expectations by corporations, oligarchs, and their political servants(“every kid college ready!” to “graduation rates must be maximized”) to the pitiful salaries, the pressures are tremendous. Also, parents are terrified of the future that awaits their kiddos and have unrealistic expectations about what schools can actually do. This adds additional pressure. The politicians, being arch-prostitutes, use this fear as a cudgel(“teachers are failing the children!”). So many feedback loops.
Having taught at the university level for a number of years before making the leap to public high school, I now understand why my college students were so poorly prepared. I await the day when the same forces that assail K-12 conquer the public universities. The escalating costs and student debt levels make them vulnerable to scapegoating by politicians. It is only a matter of time.
Definitely, I’d like to see a socioeconomic breakdown of districts who are willing to let some as yet to be determined level of programming be substituted for chemistry, biology, physics, algebra 2, trig, and calculus credits. Definitely not going to be implemented half-assedly in any $20 – $30k a year private college prep schools, that’s for damn sure. Not many people are going to come out of high school and succeed in a bachelor of science degree program with crap for math SAT scores.
Call it what it is, teach it to a decent level, same as math and science, and provide AP specializations for even higher level electives/achievers.
I suspect you are wrong about private schools, I’m sure there are those with intense math requirements, but many fairly prestigious schools some religious had less math requirements than the public schools which actually had a lot, all of them badly taught but hey …
And guess who gets into the more prestigious colleges, it’s not the kids form the public schools. Private school sometimes seems a glide path actually. Then it produces these really emotionally soft people with lots of privilege they hardly see, generally nice people though actually, much more polite than the public school kids.
”not many people are going to come out of high school and succeed in a bachelor of science degree program with crap for math SAT scores.”
I must be one of the few. I avoided math courses in HS and College like the plague. I did the minimum
college math requirement for a B.S. degree in finance with a minor in psychology and graduated with a 3.75 GPA out of 4.0 from a 4 year state university in 1980. I wish I could have gone through a comprehensive math program in high school but my parents could not afford a full time tutor.
When I was an undergraduate, my school let me use computer languages as to meet the foreign language requirement, I don’t this caught on, though–most colleges just dropped their foreign language requirement at that time or shortly thereafter (I think mine did, too)
I’ll try to take the devil’s-advocate side. I have engineering and CE degrees, and have worked in software as a semi-serious programmer for over 30 years, mostly in high-level languages that did not require any serious knowledge of algorithms, almost entirely Python for the last few years.
My experience of mathematical education in a college-prep followed by an engineering college in the 80s is that it was very poor. It mostly involved teachers going to a board and deriving equations for 45-60 minutes with little discussion of the reasons or meaning of what they were doing, and often in a nearly unintelligible accent. It was stultifying. When you lost the thread at any point, you mostly never regained it. You learned enough to pass a test, moved on, and soon forgot it. I remember learning how to perform integrals and derivatives for dozens of different functions, each with their own trick, but without ever gaining any insight as to what you might actually solve with that knowledge. It might as well have been arcane theosophy. I forgot almost everything I ever learned about calculus decades ago. I regretted it when I tried to teach myself data science a few years ago, and tried to teach myself Statistics and Calculus again, but ended the attempt after a few months after coming to appreciate the required effort versus the expected rewards.
On the other hand, the few CS courses I took were invariably interesting, fun, and led to a lucrative career. While I would rather not see mathematics de-emphasized in any way, the simple fact of the matter is that many intelligent, educated people have only the most limited understanding of advanced math, even if they went through science and engineering programs. I’m not terribly convinced that the time spent in required math classes typically leads to any lifelong understanding, and is rarely worth the time invested, practically speaking. Those for whom it is worthwhile will not need required classes.
Similar experiences on my end in engineering school for many classes, but I had a few good bits of instruction. My calculus instructors did a pretty good job of at least “visualizing” the concepts for us in imagination land.
As I stated below, the world of mathematics really opened up to me when I perceived of mathematical concepts as things rather than actions. If that makes any sense. A normal distribution could act on something as a entity unto itself rather than, “I put in these numbers and these numbers come out”. I only wish as a child I had it conveyed to me in this way.
Math became even more fun once that visualization really kicked in. Calculus with rotations of different shapes, or motions, or flows or vectors allowed this young person to imagine riding along on the edge of those.
So many good comments here. I will just confirm that my Computer Science courses in the 1980s helped me with three things: 1) logic and critical thinking, 2) an understanding of how things work, and 3) the concept of GIGO (Garbage In Garbage Out).
For #2 “understanding,” what I mean is this: I realized from many sleepless nights of coding and debugging that computers are flawed because flawed humans provide the content. Computers aren’t magic or superior as our corporate tech overlords would have most naive people believe.
This has helped me when I explain to my kids that algorithms are just code hidden behind today’s news content, e-commerce, and online censorship, and that “AI” won’t take over the world because one flaw can crash an entire program. The more complex the system the more vulnerable it is, especially due to GIGO.
Our tech overlords claim their algorithms don’t need regulation or oversight, because they’re too complicated or have proprietary information. Frank Pasquale, author of Black Box Society, and others have argued that it’s essential that the algorithms that rule us are transparent and regulated if we want a more democratic society.
My scattered 2 cents. I’m not necessarily proud to say it, but a majority of my prototyping when I was coding in a university lab was done with the help of Google searches. I’d say this was the case with a number of researchers. Not that this is/was unethical, if there is code that already does what you require why build it from scratch? Just follow the open source license and go. Though this method is useful for working out a new piece of complex software it can be dangerous if the individual does not clearly understand the thing they are utilizing. How does it work mathematically? How does it act on the data/image/sound/etc. to produce the desired result.
The above being said, I am drawn to a recent essay I read from a mathematician on the subject of math instruction. They talked about how there are certain mathematical concepts that, when learned, completely transform the way a person perceives mathematics (possibly anything else as well). Though, this hinges on the ability to understand the concept not as a process but an actual thing in the minds eye. I think the issue initially with a number of mathematical concepts is the student views the concept as a “verb” rather than a noun. The function/set/distribution “does” this, rather than “is” this.
Tying into the first paragraph. Software can be very useful to make math “real” in a way that is more accessible for people that don’t have the John von Neumann brain. However, there is still the need to understand that these concepts are actual things that act on the world, whether through data or natural law. They are not just actions. This took me a long time to understand (I’m not naturally inclined to mathematics). If software is utilized, and it should, coding a mathematical concept from scratch is actually a great way to grasp the idea. This helps to make the concept transformative and opens “headspace” for further ideas in mathematics.
Is it the desire of tech companies to teach mathematics as a means of opening peoples minds to new ideas, I imagine no, so there will have to be vigilance when assessing what the school system deems proper curriculum. Particularly if said tech companies are helping to shape the curriculum.
This article asserts that “there is still far more demand for computer science and software engineering workers than there is supply.”
Note that the job “demand” link resolves to the Bureau of Labor Statistics at https://www.bls.gov/ooh/computer-and-information-technology/software-developers.htm
This estimates that the employment growth OVER A TEN YEAR PERIOD is 284,100 jobs or about 28K new incremental jobs per year.
There will be some retirements and other exits of the workforce during the 10 year period so more than 28K new workers will be incrementally needed, but, to me, the BLS number does NOT indicate a vast need for many new software developers.
Per https://educationdata.org/number-of-college-graduates/
“During the 2015-2016 academic year, 1,920,718 Americans graduated with a bachelor’s degree.”
So with almost 2 million/year new college graduates there is a demand for about 30,000/year to work as software developers.
This suggests that about 1.5% of the new graduates will find employment opportunities as software developers.
This does not account for H1-B visas supplying even more workers.
There are other STEM jobs, but per https://www.bls.gov/spotlight/2017/science-technology-engineering-and-mathematics-stem-occupations-past-present-and-future/home.htm
“Employment in computer occupations was nearly 3.2 million in May 2009 and nearly 3.9 million in May 2015. Employment of engineers was nearly 1.5 million in May 2009, compared with over 1.6 million in May 2015.”
Over the May 2009 to May 2015, the number of engineers required grew by 100,000 over a 6 year period or about 16K per year.
And the USA labor force is estimated at 160 million in 2018.
Perhaps I am looking at these numbers incorrectly, but it appears the assumed high demand for STEM workers is NOT evidenced by the available data.
I am likewise skeptical of the “more STEM will solve all of our ills” mentality that passes for thinking.
Lack of math and physics education, coupled with some exposure to computer magic, leads too many citizens to deluded ways of thinking about the world. E.g., that self-driving cars and cryptocurrencies will somehow get around the finite nature of the planet to give us “sustainable growth”.
I guess you could spin it many ways, what I see around me that people lack is reverence for nature, but one would have to have been raised with some to even know it.
Now should it be the responsibility of the average citizen to construct a full on sustainable economy in their head? I’d tend to say no. That would indicate a complete failure of leadership and policy and the use of actual expertise, which everyone is not, if everyone is reduced to that. Although that’s about where we are.
As a professional computer system engineer, this is horrifying. Without a strong foundation in mathematics and science, students will not have a real understanding of computer science.
Knowing the idiocracy, things like Javascript and Scratch coding, building web sites with drag and drop tools or playing Minecraft will be considered as ‘Computer Science’.
Without Algebra I, there will be no understanding of “The Art of Computer Programming” by Donald Knuth.
I agree more computer science should be taught in our schools, but not at the expense of Mathematics.
I’ve always found it funny that when people who didn’t really grok something say they never needed to use it later in life. I mean, of course, if you don’t understand how to see the world in through that particular metaphor as a lens (math, philosophy, physics, etc), how would you ever expect to recognize opportunities when it might have shed light on something?
As a PhD CS type (’90 Cornell CS PhD, ’86 Rice BSEE) I can firmly attest to the INSANITY of this idea. Math — real math — is a necessary prerequisite to being good at CS. But it doesn’t work in the opposite direction. Heck, I still remember my first “Discrete Structures” (that’s basics of logic and shit) professor telling us that this was “bonehead math”. And he was right.
To treat CS as the same as real math, is to rob children-soon-to-be-adults of the life possibilities that come with real mathematics knowledge and skill.
General caveat – what follows is personal opinion, based on studying math, science and computer science in university, and then working in IT.
The problem with this is that the discussion about what to teach seldom bothers to define ‘computer science’ and when it does, it often looks like a mix of programming, the computer languages du jour, and web design and/or game design.
In my personal corner of the universe, none of those are core computer science, just as learning to drive a car or three is not automotive engineering.
Computer science does, or should, require substantial studies in math, some science courses, and theoretical or mathematical courses in computer science. It also needs courses in fundamental aspects of computing – information structures, language design, operating systems principles, numerical analysis, and probably a few other things lurking in my inherent assumptions for so long I don’t notice them.
Certainly some computer science courses have sufficient abstract mathematical content to also qualify as math courses – recursive function theory, computational complexity, numerical analysis, automata theory, applied algebra. Some other courses make significant use of math – language processors, for example, in the analysis of formal grammars, information structures in analyzing the search, sort, and modification complexities of various structures, and probably others.
That said, ‘computer science’ as a whole is neither math, nor science, as it is often taught. Science is about a cycle of experiment, hypothesis, experiment testing hypothesis, more testing, maybe a theory, experimentation trying to break the theory or extend it, and so on.
Computer science is taught in universities (I hope), it is not taught in colleges or high schools, generally. I know some people here use ‘college’ and ‘university’ as synonyms, but here a university grants degrees in academic or professional subjects such as engineering, law, and medicine while a college grants diplomas for courses teaching practical skills to become an aircraft mechanic, tool and die maker, welder, legal secretary, web designer, and the like.
(A college is also an administrative division within a university, in some cases. I was admitted to a college to take a university program in the sciences. Context usually sorts the two uses out, Paperwork was college stuff, as were residences, while course stuff, save for some traditional courses, were handled by university faculties or their departments.)
Given the fact that many topics in ‘computer science’ are not either math or science, I don’t think they should be counted as such. I also see little point in teaching computer science to pre-teens… in fact it may do more harm than good.
Why? Look into the research on the effect on thinking and expression caused by differences in learning cursive writing, learning printing, or going straight to a keyboard. Also take a peek at ‘The Informaton’ by James Gleick, which looks at how the changes in storage and retrieval of information change how we remember and think. (If you find ‘The Information’ interesting you may like ‘The Book of Nothing’ by Barrow, which explores how changes in basic concepts change how we see and deal with the universe.)
On the other hand, I think we should go to something closer to the original ‘liberal arts’ curriculum, which included math, science (er… natural philosophy), medicine, and law to go with languages and history. Communication, critical thinking, context, scientific principles, and higher numeracy are all important to mental development and skills.
One of the posters here expressed the idea that mathematical constructs are real, concrete things. I must disagree. Mathematics is abstract and arbitrary and a mathematics can be constructed based on simple axioms which define the behaviour of that mathematics. The real universe is rather less tidy than most forms of mathematics… and often easier to understand. The most difficult academic problem I faced in first year? Proving that one is bigger than zero, starting with a handful of axioms about the set of integers, none of which said anything about ordering.
What goes into a computer science degree (with a few extra items)? Looking back at an undergraduate transcript I see 11 computer science courses, some of which are also math, 11 math courses, 5 hard science courses, and a fair number of courses in soft sciences, philosophy, and history, some of which were required. Two of those courses specifically include programming as a central theme – ‘machine architecture and assembly language programming’, and ‘programming languages and applications’. You might or might not include the course where we learned about formal grammars, designed a language, and wrote a compiler, but there the language was an exercise to learn more fundamental things. Definitely not intended to churn out coding drones for massive corporate projects.
calling high school computer science (ie basic coding) the same as math is like calling carpentry the same as physics.
i code for a living.
true computer “science” is more like higher formal math. not even the analytical applied math (that of Euler/Fourier) that engineers are used to. it is highly abstract specialized math, something almost no one else ever needs or cares about. I never needed it once in my professional life. That’s why history majors, economics majors – anyone can just wash their face in the morning and become a professional coder.
I once had a LSE post grad try to teach me coding. Anything goes in this field. Half the time they just reinvent the wheel, by a new name, and thrice as more complicated than before, functionally exactly the same thing. And people have to spend months trying the navigate the new “knowledge map”.
and no, you can’t do CS without first doing real analytical math.
When talking about general education, I see no benefit to going deep into the more formal computer science as an alternative to math – it is no less daunting.
However, when it comes to learning logic or abstract thinking, I have no problem with some courses in basic data structures and algorithms substituting for some math. From my experience, working out how an AVL tree or a red-black tree works – first step by step and then in practice – was plenty of exercise for the mind, and since there is a practical “machine” aspect to it, it was much easier to find the start of the path to understanding – some of the more abstract math was simply too forbidding and unapproachable to my modest abilities.
I’m not saying that there was a direct practical value to most of it in my daily life, any more than most math I learned, but I felt it was all good foundation-building stuff.
When it comes to “professional coders” not needing any of that stuff, in my experience the problem of not understanding or caring about basic concepts like O(n) complexity does not manifest immediately – things just start chugging or crashing after a few years of crappy coding, when the load increases and more and more systems get bolted together. The original coders will often have already moved on in their career, so the problem is left to someone else to solve.
Hmmm, let’s try this slight rewording of the Florida governor’s quote on for size:
“Other than trying to keep myself and my kids from being fleeced by the Wall Street greedheads and gig-economy AlgoBros I don’t know how much I deal with math daily,” the governor said.